1 泊松方程的三种数值解法的简介
泊松方程是数学领域中一个常被运用于处理静电学、机械工程、和理论物理问题的椭圆型偏微分方程,它由法国数学家、几何学家以及物理学家——泊松发现并命名的。

泊松方程为: ()
![]()
()
![]()
方程里面的是拉普拉斯算子,的欧几里得空间。
泊松方程数值求解的方法有很多种,最常见的为以下三类:有限元法、有限差分法、有限体积法。接下来我们将重点讨论这三种不同方法的特点以及差异性。
1.1 有限元法
这里的有限元法即我们常说的Ritz-Galerkin法,那么下面我来简单介绍一下有限元法解泊松方程的主要原理:
考虑到泊松方程的物理意义,在这里可以使用最小位能原理,不难理解u是位能最小时的u的解,则位能的表达式即为:


求u的最小值这可以让我们直接联想到线性方程的解法:,想要求出X的极小值,我们转换成的极值问题,就是对展开求导,让,最后再求出X的值。

同样的,对于,我们可以将之化成,然后再对求导,让,并且使用泛函数中的虚功原理,最后,我们就能将微分形式变成变分形式:


但即便是这样,无限维的泊松方程依旧很难解出来。在这种情况之下,我们通常要考虑求出其解的近似值。所以,我们可以使用Ritz-Galerkin法,这种方法的基本思路是在中选一个N位子空间,然后在解上述变分问题。综上所述,有限元法可以分为以下几个步骤来完成:
选择出单元结构并且剖分区域
构造出基函数从而形成有限元空间
列出有限元方程并求出方程解
收敛性及误差估计
1.2 有限差分法
有限差分法和有限元法相比较起来,差别就在有限元法的第三步中,使用有限差分将微分形式变成差分形式,其余步骤都是一样的。下面我就来举出一个有限差分法解泊松方程的例子:
考虑一个椭圆方程:

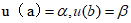
方程的差分形式是:

总结以上的内容就可以得出有限差分法的几个步骤,分别是:
(1)对求解区域进行网格划分
(2)构造逼近微分方程定解问题的差分格式
(3)差分方程的解法
(4)收敛性和稳定性的研究
1.3 有限体积法
有限体积法其实可以被理解为广义差分法。传统的差分法只限于矩形网络,而矩形网络逼近一般误差会比较大,也不是很灵活。所以可以考虑将差分法推广到三角网络,这就是广义差分法这就是所谓的有限体积法。

考虑泊松方程第一边值问题:
![]()
设是矩形区域,=为的边界,。
![]()
对区域作均匀的矩形剖分,每个矩形称为单元,记作K,节点为,记x,y方向步长分别为,

![]()
以表示所有矩形单元边中点的集合,表示所有矩形重心的集合,,。
![]()
再作的对偶剖分,记为,它由围绕节点的矩形域,的矩形域和的矩形域组成,记[0,1]区间上的两个Gauss点为;令,,则对偶剖分的具体作法如下:
的作法:设,为Q所在单元的顶点,为Q所在单元的边的中点。设是直线段的交点,则依次连接,就得到一个围绕Q的矩形域,记为(见图一)。
的作法:设为M所在的两个单元的所有顶点。设是直线段的交点,则依次连接就得到一个围绕M的矩形域,记为(见图2)。
的作法:设,为P所在的四个单元的所有顶点。设是直线段的交点,则依次连接就能得到一个围绕P的矩形域,记为(见图三)
|
图3 |

试探函数空间取为相应于矩形剖分的双二次有限元空间,即对每一。相应的基函数分别为满足下列条件的分片二次多项式:
。
检验函数空间取为相应于对偶剖分的分片常用函数空间,即对每一。相应的基函数分别为
。
以下我们定义有限体积元的格式。
采用上面构造的和相应的双二次元体积格式为:求,使得
,
或等价的
其中
如图一,图二,图三,是其相应对偶单元的边界。右端积分可以分解成这些线段上的积分和,每个积分都很容易算出,从而可以得到以为未知量的线性代数方程组。
有限体积法和有限差分法最大的区别在于有限差分法使用了广义导数,并将区域剖分对偶化。
2 多种泊松方程数值解法的介绍
上文已经给出了有限元法、有限差分法、有限体积法的基本步骤,在这里,我们将根据这些步骤来对一维和二维的泊松方程进行求解以及对误差进行估计。
2.1 一维泊松方程的数值解法
2.1.1 一维泊松方程区域剖分及构造有限元空间
这里,将之剖分
我们定义
2.1.2 建立方程组并求解
为了得到有限元方程和差分方程,我们可以从Ritz法出发,构造试探函数即基函数,如下:
是由组成的函数空间,其中 同时,我们来定义:
对于有限元方程、有限差分方程、广义差分方程,我们可以通过,求来求泊松方程的数值解。
这样我们可以得到数值方程如下:
有限元方程:
其中
有限差分方程:
有限体积法方程:
接下来就是解方程组:
根据这三个方程就可以得到一组线性代数方程,从而就可以得到三个矩阵
其中有限元法,有限差分法,有限体积法
解此矩阵即可,可得到:
对于稳定性和误差估计而言:
对于稳定性,我们可以使用
误差估计,我们可以使用
2.2 二维泊松方程的数值解法
2.2.1 二维泊松方程区域剖分及构造有限元空间
这里,
对于轴,部分和一维的一样,
对于轴,
我们定义:
并设定,
对于每个子区域,把它分为六个小区域
如图:
