在机械加工中，误差是不可避免的，只要误差在规定的范围内即为合格品，否则就为不合格品。通过误差分析，可找出产生误差的主要原因，掌握其变化的基本规律，从而了解、预测和监控过程的运行和水平，来减少加工误差，提高加工精度。
统计过程控制主要解决两个基本问题：一是过程运行状态是否稳定，二是过程能力是否充足。前者可利用控制图这种统计工具进行测定，后者可通过过程能力分析来实现。统计过程控制理论的应用是从制造业的加工过程开始的，但是其应用已扩展到各种过程，如设计过程、管理过程、服务过程等。
机械加工精度是指零件加工后的实际几何参数与理想几何参数的符合程度。符合程度越高,精度越高。生产中,加工精度的高低常用加工误差的大小来表示。加工精度越高,则加工误差越小;反之越大。
在机械加工中,由机床、夹具、工件和刀具组成一个工艺系统。此工艺系统在一定条件下由工人来操作或自动地循环运行来加工工件。因此,有多方面的因素对此系统产生影响,引起加工误差,归纳起来有以下几方面的因素:
(1)加工原理误差。是由于采用了近似的加工原理(如近似的刀具或近似的加工运动)而造成的误差。
(2)安装误差。是指工件定位、夹紧时所产生的误差。
(3)工艺系统的几何误差。是指机床、刀具和夹具本身在制造时所产生的误差,以及使用中产生的磨损和调整误差。
(4)工艺系统的受力变形。机床、夹具、工件和刀具在受切削力、传动力、离心力、夹紧力、惯性力和内应力等作用力下会产生变形,从而破坏了已调整好的工艺系统各组成部分的相对位置关系,导致了加工误差的产生。
(5)工艺系统的受热变形。在加工过程中,由于受切削热、摩擦热以及工作场地周围热源的影响,工艺系统的温度会产生复杂的变化,工艺系统会发生变形,改变了系统中各组成部分的正确相对位置,导致了加工误差的产生。
(6)调整误差。在机械加工的每一工序中,总要对工艺系统进行这样或那样的调整工作。由于调整不可能绝对地准确,因而产生调整误差。
(7)测量误差。零件在加工时或加工后进行测量时,由于测量方法、量具精度以及工件和主客观因素(温度、接触力)都直接影响测量精度。
过程控制是指为实现产品生产过程质量而进行的有组织的、有系统的过程管理活动，其目的在于为生产合格产品创造有力的生产条件和环境，从根本上预防和减少不合格品的产生。
其内容主要包括：
（1） 过程分析和控制标准
分析影响过程质量的因素，确定主导因素，并分析主导因素的影响方式、途径和程度，据此明确主导因素的最佳水平，实现过程标准化；确定产品关键的质量特性和影响特性的关键过程，建立管理点，编制全面的控制计划和控制文件。
（2） 过程监控和评价
选择适宜的方法对过程进行监控；利用质量信息对过程进行预警和评价；利用过程性能指数和过程能力指数对过程满足技术要求的程度和过程质量进行评定。
（3） 过程维护和改进
过程控制通过对过程的管理和分析评价，消除过程的异常因素，维护过程的稳定性，对过程进行标准化，并在此基础上，逐渐减小过程固有的变异，实现过程质量的不断突破。
控制图是对过程质量特性值进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图。控制图是如何贯彻预防原则的呢？这可以由以下两点看出：
（1）应用控制图对生产过程不断监控，当异常因素刚一露出苗头，甚至在未造成不合格品之前就能及时被发现，在这种趋势造成不合格品之前就采取措施加以消除，起到预防的作用。
（2）在现场，更多的情况是控制图显示异常，表明异常原因已经发生，这时一定要贯彻“查出异因，采取措施，保证消除，不再出现，纳入标准。” 否则，控制图就形同虚设，不如不搞。每贯彻一次（即经过一次这样的循环）就消除一个异常因素，使它不再出现，从而起到预防的作用。
在实际加工中，影响加工精度的因素往往是错综复杂的，仅用单因素分析法是不够的，而要利用统计分析的方法进行综合分析，才能较全面地找出产生误差的原因，掌握其变化的基本规律，从而实现对整个生产过程进行预测及监控的目的。
以实际加工出来的工件尺寸X(实际上是一段很小的尺寸间隔)为横坐标,以工件的频率y(频数与这批工件总数之比)为纵坐标,就可得出该工序工件尺寸的实际分布图（直方图）。再由直方图的各矩形顶端的中心连成一光滑的曲线,即实际分布曲线,如图一所示。
图一 直方图
当一批工件总数极多时,零件又是在正常的加工状态下进行,没有特殊或意外的因素影响,如加工中刀具突然崩刃等,则这条分布曲线将接近正态分布曲线,如图二所示。因此,生产中,常用正态分布曲线代替实际分布曲线进行分析研究。
图二 正态分布曲线
正态分布曲线的数学关系式为：
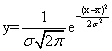
式中:
X为各零件的实际尺寸
表示一批零件的尺寸的算数平均值，它表示加工零件的尺寸分散中心。
y表示零件尺寸为X时所出现的概率,即出现尺寸为X的零件数占全部零件数的百分比。
σ为一批零件的均方差。
1）验证工艺能力系数
工艺能力系数表示了工艺能力的大小，表示某中加工方法和加工设备能否胜任零件所要求的精度的程度。
2）计算一批零件的合格率和废品率。
3）误差分析
从分布曲线的形状、位置可以判断加工误差的性质，分析各种误差的影响。
由于加工中随机误差和系统误差是同时存在的，而作分布曲线的样本必须是一批工件加工完毕后随机抽取的，是没有考虑工件加工的先后顺序，故很难把随机误差与变值系统误差区别开来，也不能在加工过程中及时提供控制精度的资料。
统计过程控制（简称SPC)是应用统计技术对过程中的各个阶段进行评估和监控，建立并保持过程处于可接受的且稳定的水平，从而保证产品与服务符合规定的要求的一种质量管理技术。它是过程控制的一部分,从内容上说主要是有两个方面:一是利用控制图分析过程的稳定性,对过程存在的异常因素进行预警;二是计算过程能力指数分析稳定的过程能力满足技术要求的程度,对过程质量进行评价。
对于计量数据而言，常见的控制图是均值-极差控制图，即
控制图，将一批零件依加工顺序按每m个作为一组（ 顺序小样本（4～6个））进行分组，以小样本组序号为横坐标， 分别以每组零件的平均尺寸和每组零件的极差R （ 组内工件的最大尺寸与最小尺寸之差）为纵坐标就可得到X点图和R点图。X点图体现了变值系统性误差的变化趋势，而R点图则反映出随机性误差及其影晌。
