5.2 着法的生成
着法即为棋子的走法,象棋中,对弈双方具有相同的子力,不同类型的棋子有不同类型的走法,也会存在了一定的限定,比如常说的别马腿,填象心,为象棋增加了趣味性和对抗性。在项目中,着法生成其实是最为重要最为核心的部分,在每一次算法迭代的过程中都会调用大量的着法生成。该项目也依据不同类型的棋子做出了不同的着法生成方案,以满足着法生成的效率。
棋盘如图5-2-1:
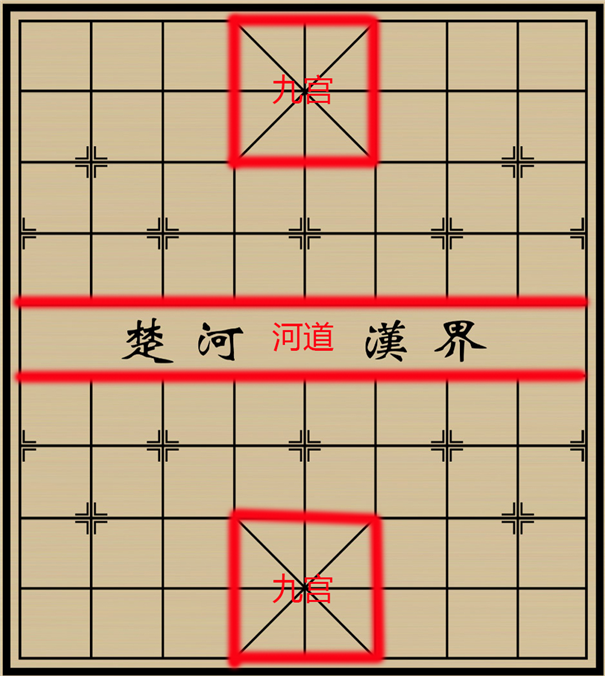
图5-2-1 棋盘
着法生成表(目标位置无本方棋子)见表5-2-1:
|
将(帅) |
士 |
象 |
马 |
车 |
炮 |
卒(兵) |
|
于九宫内上、下、左、右每次可直行一个单位长度。 |
于九宫内斜行(可以选择九宫内当前位置任意斜对角位置) |
象走“田”,即走当前位置到棋盘内任意斜对角两个单位长度的位置; 填象心:“田”字中心有子不可移动 |
马走“日”,可以将日看成两个棋盘格子构成,棋子当前位置为“日”字左下角或右下角位置,“日”字顺时针分别旋转90°、180°、270°皆为可到达的位置。 别马腿:若有子位于“日”字中棋子当前位置正上方一格位置,马于该方向不可移动 |
车可直行到棋盘内上、下、左、右直行任意单位长度,直到遇到其他棋子。 |
炮可直行到棋盘内上、下、左、右直行任意单位长度。 翻山炮:若在敌方棋子与炮之间只有一个棋子相隔,炮可吃此敌方棋子。 |
卒(兵)在过河前只能朝敌方阵营前进,过河后,每次可横向左右行走一个单位长度。 |
表5-2-1
5.2.1 棋盘数据的存储与生成
棋盘本身应当是一个九列十行的交叉点构成,在项目中由于以后的棋盘需要速度的支撑,将棋盘扩充为16*16(256大小的一维数组做二维)的棋盘,那么在换行运算中只需加减十六,在换列时只需加减一,同时也解决了边缘问题,棋盘四周的数据都存为零,只要棋子触碰到为零的区域就代表着越界,从而方便了以后的越界判断。在棋子存储方面,同样为了方便以后的位运算,红棋数据为16-31,黑棋数据为32-47,这样存放就可以通过位与16不为0即为红棋,位与32不为0即为黑棋迅速进行判断。
5.2.2 车炮着法的生成
车炮的走法其实不多:车只能直行,方位上下左右,遇到棋子再做判断是否产生吃子的状态;炮也只能直行,只有遇到第二个子的时候才做吃子判断,若不能吃子,则只能做当前位置到第一个遇到的子的位置之间的移动。但能走的位置却是最多的,因此不能简单的采用循环判断,提升效率的方案往往是牺牲空间来换取时间,项目常用的方法是采用位棋盘,所谓位棋盘,实际是做了一张记录了所有棋子位置状态和车炮所在位置能走到位置的记录(只关心棋子的位置信息,故在棋盘中有子为1,无子为0),位棋盘分为横向和纵向的,分别代表一行和一列的情况,一行是9*8*2^9的大小,纵向是10*9*2^10的大小,可见占用空间实际是非常大的,换取了一定的效率提升,但最终还是将其舍去。
5.2.3 马着法的生成
在马着法的生成中,我做了一个辅助数组,如下:
static int mastep[4][2] = {
{ -33, -31 },
{ 31, 33 },
{ -18, 14 },
{ -14, 18 } };
马的走法共有八个位置,数组中的每一项分别代表在棋盘中的移动,最终马能否走到目标位置还决定于是否存在“别马腿”的现象,对于“别马腿”的判断也做了一个辅助数组,如下:
static int mahinder[4] = {-16, 16, -1, 1};
存在四个“别马腿”的位置,与上面的移动位置相对应(mahinder[0]与mastep[0]相对应,依次类推)。
若移动位置在辅助数组中、不越界、无本方棋子,并且不存在“别马腿”,则为有效的着法。
马着法判断方式如图5-2-3-1:
 |
是
 |
|||
否
 |
否
![]()
是

表5-2-3-1 马着法判断流程
5.2.4 象的着法的生成
乍一看,象的着法与马类似,代码应当大同小异,实则存在差异。象在所处位置的移动方案总共有四种,但因其在边界的情况很多,所以对象的法做了特例性的处理。通过观察发现两方的象均不能过河,在自己的移动范围内的所有位置实际只有七个,边界位置能够移动到的位置实际只有两种情况,中心位置才具有四种情况,为了避免过多的判断,为边界的六种状态做了一个总表(手动填充,篇幅较大,代码就不贴出了)。
象着法判断流程如图5-2-4-1:
 |

是
 |
![]()
否

否

是
图5-2-4-1象着法判断流程
5.2.5 将士卒着法的生成
将(帅)士卒(兵)只有最为简单的几种着法,将(帅)和士只能在九宫格内移动,移动时只需判断是否存在吃子。卒(兵)需要进行是否过河的判断,过河卒(兵)会增加横向移动一格的着法,在卒(兵)的过河的判断上红方只需判断目的位置行是否大于7,黑方只需判断是否小于8,其实便是行与8做位与操作即可判断。
5.3 局面评估
局面评估分为整体局面的评估和单步局面的评估,顾名思义,单步局面即这一步之后预计局面得分,整体局面评估即为双方子力的比较。在不同的整体局面的情况下也会影响到单步局面的选择。在对每个棋子子力的衡量上,需要随不同局面进行变化,价值关系应当是如下关系:
将(帅)>车>马、炮>士、象>卒(兵)
但在卒(兵)过河后,子力应当得到明显提高。
下面是项目中子力的初始基值见表5-3-1:
|
将(帅) |
车 |
马 |
炮 |
士 |
象 |
卒(兵) |
|
1500 |
100 |
80 |
80 |
60 |
60 |
10 |
表5-3-1 子力初值设定
5.3.1 单步局面评估
对于单步局面的评估,我采用了:
单步得分=目标子子力+本方移动子力*K;
K:若目标子处于被保护状态,则K为1,否则为0
这样确保了评分的准确,每次移动不是随意吃子和得到表面上的得分,能够为未来棋子移动推算提供服务。
5.3.2 整体局面评估
整体局面的评估十分简单,即为将本方所有子力之和相加,公式如下:

Code=;
Code为局面分,stonecode[i]代表每个棋子的分数。
5.4 博弈程序的生成
博弈程序是整个项目的核心,一个好的博弈程序算法能够使得ai显得更加智能,运算的也更加迅速。该项目的博弈程序即为棋子ai着法的自动生成。该项目的博弈程序源于经典的最小值最大算法,经过一定的优化演变而来。
5.4.1 玩家走法生成
玩家走法的生成实际工作实际就是将玩家的走法意愿正确的通过游戏界面显现出来。整个过程包含几个模块:触发点击事件、确定选择棋子、确定移动位置、判断能否移动、移动。整个工作流程如图5-4-1-1:
 |
否
 |
能
 |
图5-4-1-1 玩家棋子移动流程
5.4.2 ai走法生成
Ai走法生成中我用了四层迭代(效果一般),最为基本的算法是最小值最大算法。算法可以这样理解,当ai的回合开始的时候,ai想要得到n步后的是最小分最大,而下一步是由玩家来操作,玩家想要得到的是ai在n-1步之后ai得到的最大分最小,最小最大算法的理解如图5-4-2-1:
 |
|||
 |
|||
![]()
 |
|||

图5-4-2-1 最大值最小值算法
由此,便可以通过间接递归调用的方式产生最大值最小的算法,进行ai移动的推算。该项目基于此进行了优化,后续部分介绍。
5.4.3 算法优化和窗口裁剪
算法优化的主要工作是在每一步生成之后对局面分选择合适的方案进行排序,使得排序后的走法数组更快的能找出最优解。
窗口裁剪的方案很多,所谓窗口裁剪就是找到有效剔除非最优解的方案来缩小搜索范围实现快速搜索博弈树。项目中采用了杀手着法和历史表启发的启发式算法来进行窗口裁剪。
杀手着法:项目设置的杀手着法队列的大小为4,即存放程序运行起来之后的四个使得算法产生相对最优解(对窗口产生截断)的走法。在开始搜索的时候先进行杀手着法的搜索,使得窗口得到大幅度的裁剪(即递归当中的最大值和最小值的差值变小)。
历史着法启发:为所有搜索过程中产生截断的走法(走法=起始点+目标点*256)累计次数,在走法排序的时候采用冒泡排序(只排前十四个),排出前七个历史截断次数最多的走法和前七个单步得分最高的走法。通过排序方案,可以使得在搜索树的时候就会产生很大的概率使得很早就产生很好的窗口裁剪效果,从而快速找到最优方案。
算法方面基于最大值最小值算法,最后项目做出了一定的优化,使用了alpha-bate(将最大值最小值算法的间接递归合并为直接递归)算法,在alpha-bate算法的基础上采用了pvs主要变例搜索。
关于pvs主要变例搜索的思想是:因走法经过排序,对本方具有优势的走法都会很快被搜索到,这些走法也通常都是好的走法,如果产生了较好的排序方案,那就可以产生一个大胆的假设,即第一步就很有可能是最好的走法。基于以上设想,pvs主要变例搜索就是每次先完整搜索第一步,直接将窗口裁剪为第一步所得结果,再进行后续的搜索,直到产生比该结果更好的结果才继续向下搜索。
Psv主要变例搜索如图5-4-3-1:

搜索深度<=0
搜索深度>0
 |
图5-4-3-1 psv主要变例搜索
5.5 悔棋和还原功能的实现
悔棋也是象棋设定中非常重要的一环,不同于比赛竞技,象棋类的程序总体是为用户提供一个轻松愉悦的休闲环境,不要求玩家每一步都十分周密和严谨,因此,从一开始的象棋软件就具备悔棋的功能。
该项目的悔棋和局面还原功能是通过一个vector容器实现的,在每一次棋子移动的时候,都会将移动的棋子的编号,被吃的棋子的编号,起始位置和目标位置记录到vector中。每次悔棋都会弹出vector两个元素,每次弹出元素时,就将移动棋子还原到起始位置,被吃棋子还原到目标位置,在修改相应的图片、棋盘等数据,棋局就能够还原到原来的状态。