引言 在十三五规划中将开放作为五大发展理念之一，2014年广州港完成货物吞吐量5亿多吨，位居世界港口第六位，虽然广州港口取得了如此辉煌的成绩，但是相对于上海港、宁波港、鹿特丹港、新加坡港等世界一流港口还有一定的差距。在这样的国内国际环境下，以广州港口为研究个例，然后对广州港口与经济进行数据分析，一方面了解当前广州港口对经济增长的影响，另一方面为今后广州港口的发展方向提供数据性的依据，进而对广州港口的可持续发展提出对策。

　　一、研究指标的选取

　　港口的货物吞吐量是由货物的进口量和出口量组成，它反映的是一个港口的运输能力以及货物周转的速度，是一个港口生产力的重要指标。所以说，一个港口物流的发展情况能够从货物吞吐量的多少反映出来。GDP(国内生产总值)是一个国家或者一个地区在一定时期内衡量一个国家或者一个地区国民经济发展规模的重要指标。GDP总量是由第一产业、第二产业、第三产业的产值构成，也可以说是三大产业的产值之和构成了一个国家或者一个地区的GDP总量，三大产业所占GDP总量的不同反映了一个国家或者一个地区在一定时期内的经济发展规模。所以在研究港口物流与区域经济增长关系时，我个人选取了港口货物吞吐量、GDP、三大产业产值这些数据指标作为研究数据具有一定的可比性和合理性。

　　二、一元线性回归模型的构建

　　在本文中，我个人选取了2005年-2014年广州港口近10年的货物吞吐量、2005年-2014年近10的GDP和三大产业的产值作为研究数据，通过对GDP总量和港口货物吞吐量进行一元线性回归分析，得出GDP总量和港口货物吞吐量的相关性关系大小，并通过得出的相关性大小来判断港口物流对区域经济的影响程度，由此为港口物流推动广州地区经济发展提供数据依据，进而对广州港口及港口物流今后的发展方向提出一些可行性的对策。

　　表 1-1 2005年-2014年广州港口货物吞吐量、GDP、三大产业产值的数据表

　　货物吞吐量：万吨 ; 产值：亿元

年份	货物吞吐量（X)	GDP(Y)	第一产业（Y1）	第二产业（Y2）	第三产业（Y3）
2005	27283.03	5154.2283	130.2159	2045.2183	2978.7941
2006	32815.77	6081.8614	128.5029	2441.516	3511.8425
2007	37053	7140.3223	149.8737	2825.7805	4164.6681
2008	36954.04	8287.3816	169.1849	3227.8717	4890.325
2009	37549	9138.2135	172.2837	3405.1588	5560.771
2010	42525.95	10748.2828	188.5645	4002.2658	6557.4525
2011	44769.53	12423.439	204.542	4576.9763	7641.9207
2012	45125.15	13551.2072	213.762	4720.6504	8616.7948
2013	47266.86	15497.2334	228.463	5270.086	9998.6844
2014	50097.49	16706.8719	218.6993	5590.9683	10897.2043

　　表1-1的数据来源于：广州统计信息网:http://www.gzstats.gov.cn/

　　表1-1中的X表示广州港口不同年份的港口货物吞吐量，Y和Y1、Y2、Y3分别表示广州地区不同年份的GDP、第一产业、第二产业、第三产业的产业总值。

　　根据表1-1中的数据，以广州地区2005年-2014年的GDP总量作为Y轴，以2005年-2014年广州港口货物吞吐量作为X轴，将表1-1中的数据输入Excel软件，利用Excel做出广州港口货物吞吐量和GDP总量的散点图。

　　如下图：

　　图1-1广州市2005年-2014年GDP总量与港口货物吞吐的散点图

根据图1-1可知：2005年-2014年期间广州市GDP总量与港口货物吞吐量围绕一元线性直线上下波动，大体呈现出正线性相关关系。所以可以构建一元线性回归模型为：(2-1)，是因变量用来表示广州2005年-2014年的GDP总量(单位：亿元)，是自变量用来表示2005年-2014年广州港口的货物吞吐量(单位：万吨)。,是未知数，其中为常数项，为港口货物吞吐量对GDP总量的变动率。一元线性回归方程反映的是一个自变量与另一个因变量之间的线性关系。但在一元线性回归模型中自变量对应的因变量不是一个确定的值而是一个取值范围。

　　三、广州港口货物吞吐量和GDP总量的回归分析

　　根据表1-1中的数据，利用SPSS19.0软件把数据导入，以广州2005年-2014年GDP总量作为被解释的变量，以广州2005年-2014年的港口货物吞吐量为解释变量输入软件进行数据计算，得出的分析结果如下：

　　表2-1 ： 广州市货物吞吐量对GDP的回归模型汇总

R	R 方	调整 R 方	标准 估计的误差	更改统计量
				R 方更改	F 更改	df1	df2	Sig.
0.966	0.934	0.926	1084.0280073	0 .934	113.432	1	8	0.000

表2-2 ： 广州市货物吞吐量对GDP的方差分析
模型		平方和	df	均方	F	Sig.
1	回归	1.333E8	1	1.333E8	113.432	0.000
	残差	9400933.765	8	1175116.721
	总计	1.427E8	9
a. 预测变量: (常量), 货物吞吐量。 b. 因变量: GDP

　　表2-3： 广州市货物吞吐量对GDP的回归系数

		非标准化系数		标准系数	t	Sig.	B 的 95.0% 置信区间
		B	标准 误差	试用版			下限	上限
	(常量)	-11442.417	2086.054		-5.485	0.001	-16252.866	-6631.969
	货物吞吐量	0.546	0.051	0.966	10.650	0.000	0.428	模型

由表2-3可知，把得出的相关数据代入(2-1)中，可以得出广州港口货物吞吐量对GDP总量的线性回归方程是：(3-1)。

　　模型分析如下：

　　(一)一元线性回归模型的经济意义分析

这个模型的经济意义是：广州港口货物吞吐量每增加1万吨，GDP总量将会增加0.546亿元，常数项 ，它的经济意义是：在港口货物吞吐量等于0的情况下，GDP总量为-11442.417亿元，即GDP总量将减少-11442.417亿元。由此可以知道，广州港口货物吞吐量的增加能够促进广州地区经济总量的增加，两者具有线性正相关关系。

　　(二)相关系数和一元线性方程拟合程度的评价

　　1.相关系数和可决系数的划分依据

由数学知识可知相关系数R的取值范围为，它的密切程度划分为：

为不相关，时为低度相关， 时为显著相关，时为高度相关。

可决系数R²的取值范围 ，越接近于1说明方程的拟合程度越好,越接近与0说明方程的拟合程度越差。

　　2.相关系数和方程拟合效果的评价

根据表2-1的模型汇总表和相关系数、可决系数的划分依据可知，相关系数，说明了港口货物吞吐量与GDP总量的相关关系高度相关，可决系数这也说明了方程的拟合效果很高。

　　(三)一元线性回归模型的检验

　　1.Sig值的划分依据

　　Sig的值是用来判断方程和参数的显著性的，Sig的值通常与0.05相比较，如果Sig的值大于0.05，则可以接受原来的假设，方程或参数不显著，如果Sig小于0.05 ，则可以拒绝原来的假设，接受备选假设，可以认为参数或方程显著。

　　2.显著性的检验

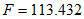
由表2-2 方差分析表中，统计量,与之相对应的Sig的值是0.00，它小于0.05，因此应该拒绝原来的假设，说明方程具有显著性。对于参数的显著性检验，由于a 是常数项，它的重要程度不如b，所以对 b进行显著性检验，由表2-3系数表可以知道,b对应的t的值是10.650，它对应的Sig值是 0.00，小于0.05,说明该模型的参数也是显著的。

　　基于以上各显著性的检验，方程(3-1)的线性模型是有效的，所以得出的结论是：广州港口货物吞吐量的增加可以引起广州GDP总量的增长，在2005-2014年间，广州港口的货物吞吐量每增加1万吨能带动广州市GDP总量增长0.546亿元。

　　四、广州港口货物吞吐量对三大产业的回归分析

　　为了研究港口货物吞吐量对三大产业产值的影响哪个最为突出，以表1-1中以X港口货物吞吐量作为自变量，第一产业、第二产业、第三产业的产值Y1、Y2、Y3分别为因变量输入SPSS19.0软件，分析过程和(3-1)一样，在此处省略，得出的最终结果带入(4-1)、(4-2)、(4-3)之中，根据表3-1中的相关数据，得出的一元线性回归方程依次如下：

　　表3-1 广州港口货物吞吐量对三大产业的回归分析有关数据

产业	R	R²	F值	F对应的Sig值	a的值	b的值	系数其t的检验的Sig的值
第一产业	0.954	0.909	80.366	0.00	-16.583	0.005	0.00
第二产业	0.980	0.960	193.496	0.00	-2951.853	0.168	0.00
第三产业	0.958	0.918	89.642	0.00	-8473.711	0.373	0.00

　　港口货物吞吐量与第一产业产值的回归模型是：

(4-1)

　　港口货物吞吐量与第二产业产值的回归模型是：

(4-2)

　　港口货物吞吐量与第三产业产值的回归模型是：

(4-3)

结合方程(4-1)、(4-2)、(4-3)和表(3-1)可以知道，广州港口货物吞吐量每增加1万吨，则广州地区第一产业、第二产业、第三产业的产值分别增加0.005亿元、0.168亿元、0373亿元，说明了广州港口货物吞吐量对第三产业贡献率最大，其次是对第二产业，对第一产业的贡献率最小。港口货物吞吐量与第一、第二和第三产业的相关系数分别为0.954、0.980、0.958，因为它们的相关系数都比0.80要大，所以它们的相关系数都很高，而且第二产业的相关系数是最高的，第三产业和第一产业的相关系数相对较低。港口货物吞吐量与GDP的可决系数分别是0.909、0.960、0.918，三个数据都接近与1，说明了广州港口货物吞吐量与第一产业、第二产业、第三产业的一元线性方程拟合效果都很好，并且货物吞吐量与第二产业的拟合效果略高于其他两大产业。

根据表3-1中的数据可知：第一产业、第二产业、第三产业的统计量的值分别是：80.366、193.496、89.642，他们对应的Sig值都是0.00而且都小于0.05，说明了它们相对应的方程也是显著的。货物吞吐量与三大产业对应的的系数对应t的检验值即Sig的值分别是：0.00、0.00、0.00同时他们的三个对应的值也都小于0.05，所以方程的系数也是显著的。具有较强的统计学意义，模型构建也是合理的。